Stereo-vision calibration

I've noticed a weird distortion during field-testing the new graphics on the AR glasses: signs that should have been far away looked way too close, but they got further as I approached them. Pupil distance didn't seem to fix it without introducing other issues.

So I've decided to finally properly calibrate the projection parameters.

Content warning:
All drawings are really badly made with KolourPaint (KDE's version of MSPAINT).

3D projection intro

If you have a game development or rendering background, you may want to skip this section. It's mainly useful for people who don't deal with affine projection matrices on a daily basis.

Plato's cave

Let's build the digital version of this old classic:

( 4edges, An Illustration of The Allegory of the Cave, from Plato’s Republic, cropped by me, CC BY-SA 4.0 )

Projecting the world to a rectangle

In the most common case, we need to display a 3D world on a 2D rectangle (the screen). The eye is already 2D (topologically), so if we only consider a single eye, we can achieve the exact same image on the retina as a real 3D scene would.

OK, let's start with the classic schoolbook drawing to set the tone:

This drawing is horrible and explains nothing. Maybe the fundamentals: all "light lines" cross at the middle of the pupil (that's the only place light can enter the eye after all), and that the projected image is inverted.

We will work with proper cross sections instead:

First of all, the above scene is 2D (circles and rectangles), and the eye projects the scene down to 1D (segments). This will make subsequent drawings way simpler, and I promise you it works exactly the same way with 3D => 2D projection.

We assumed (spherical frictionless cow-style) an infinitely small pupil and no lenses, but these do not change rendering.

With that out of the way, you can see that the "scene" of the three rectangles get projected down to two segments. The orange rectangle is occluded by the blue one, so it doesn't have a projection.

Now take a look at the next two images:

Notice how the scene is very different (two segments instead of three rectangles), but the eye sees the exact same thing.

It doesn't matter where exactly the colored segments are, as long as the "light lines" are the same, the eye will see the same thing.

Screens and coordinates

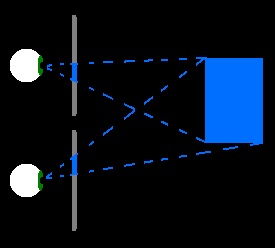
Now that we know all this, a let's introduce a screen:

To "draw" a virtual scene and make the eye "believe" it sees the virtual scene, we project the scene onto the screen and draw the proper segments. Then the eye does another projection, and the result is the same as if it saw actual objects.

The projection to the screen is done by finding the "light lines" between the virtual object and the center of the pupil, intersecting these lines with the screen's line, and drawing the image on the screen accordingly.

How to do that intersection thing? Sounds hard and math-heavy? It's not hard, but it does need some math, namely coordinate geometry. Let's consider the following Cartesian coordinate system:

The axes are weird, and sorry for this, but this will follow convention of typical 3D axes.

So how does this help? We can find each intersection by getting the coordinates of the originating point (e.g. one of the rectangle corners), and dividing its x coordinate with its z coordinate. This will give us the line's intersection with the z = 1 line.

(Deriving this is left as an exercise to the reader)

This is basically how all 3D rendering works. You try to arrange everything with transformations so that the eye is at the origin, looking down the Z axis, and the screen to project to is at Z=1, spanning XY. Then you get the 2D screen coordinates of the objects by dividing X and Y with Z. Then you fill them or draw them with textures or whatever.

Field of view

Real screens have a resolution and a size. Shocker, I know, but this is important. Once you projected your objects to the z=1 screen space, how do you make sure that the actual piece of flesh (a.k.a. the user) will project that image to their retina like you intended?

If you don't do it right, the following can happen:

The important metric here is field of view, an angle between the eye and the two sides of the screen. This has to be set up in the virtual scene transformations so it's the same.

Notice how you can have the same field of view with different sized screens if you sit closer or further.

Binocular depth perception (biology)

Most humans have two eyes, and most of them use those two eyes to determine the distance of objects. (Among a lot of other methods)

It is very important to get these right in Virtual Reality use-cases, because the brain is using all depth algorithms at once, and if they don't agree, the best that can happen is it looks fake and disorienting, the worst is you get nauseous.

So you really do need stereo rendering, and you have to do it right.

Convergence angle

The simplest depth algorithm is by determining the convergence angle: the angle difference between the two eyes when they are looking at something.

An example with points:

Stereopsis

The convergence angle method works to some 10-15 meters. After that the angle gets smaller than the typical alignment error of the eyes themselves, and the brain just considers it "infinite".

However, there is another algorithm in the brain: stereopsis. It is not an "absolute" method like the convergence angle, but a relative one: you can tell which objects out of two is farther away, and by how much.

This is incredibly accurate, up to something like 500 meters or more. (So any rendering has to be just as accurate).

Consider the following example:

Even if there are no other depth cues (like occlusion, size, context or convergence), it is still known to the viewer that purple is farther away than blue.

Stereoscopic rendering

Proper Virtual Reality and Augmented Reality is binocular, i.e. it makes a stereo image, i.e. it has two displays, each for one eye, and they display different images:

There are some parameters that need to be right (same in the virtual and the flesh world), or else the picture will not look right.

Screen center alignment

The physical screens in the physical world need to be aligned, such that if the user looks at their centers with both eyes, the convergence angle is exactly 0°, actual infinite depth (practically 1km+).

Most AR/VR glasses have clever optics to make sure this is always the case, no matter the distance between the pupils. You can check it out by moving the glasses left and right, and the picture will stay in place. Much like a red dot or holo sight.

If the glasses are not well aligned (common error is a small angle between the two), this needs to be compensated for in software: the rendered picture needs to be offset a bit.

Pupil distance

Even though the optics will make sure that the screen is exactly in front of the eye all the time, we still need to know the pupil distance in the virtual world for depth perception to work correctly.

See these cases:

Correct rendering is easy to achieve, fortunately: make pupil distance configurable, and when you are rendering the scene for the different eyes, put the virtual camera half a pupil distance to the left or right.

If you don't get it right, objects will look proportionally farther or closer than intended, and their perceived position will change as you get closer or further from them.

The problem I had

I'm going to spoil it for you: my FOV setting was wrong (by half a degree!), and when I first tried to compensate it with adjusting the pupil distance setting (thinking maybe I measured it wrong, or there's something funky going on with the AR glasses' optics) gave me this weird distortion (exaggerated):

If I set the pupil distance to the correct value, the depths looked wrong. If I set it to the weird compensated value, the depths were correct, but object sizes looked wrong. In fact, as they were getting closer, they became bigger? I don't know, it was very confusing, and instantly destroyed the sense that the "holograms" were actually part of the world.

The worst part is that I didn't realize what the actual problem was, it just "looked wrong". So I methodically recalibrated every parameter I could. I spent a few hours trying to compensate lens centering error (more on this later), actually measured my pupil distance with a caliper, and also calibrated the FOV by looking at an object of known distance and size and aligning it to the edges of the screen.

This worked, and now things look correct. The sensation is weird too, the whole 3D world just clicked in place, and now looks more real than ever.

Lens centering adventures

These cheap AR glasses I use will never be 0.1° correct in their alignment, so some software calibration is necessary. Interestingly, small misalignment doesn't matter in a VR setting where the only thing the user sees is the render. This is because stereopsis (the relative, precise one) is controlled by the render itself, and convergence angle measurement (in the eyes and brain) is just not that precise. In fact, small errors, even vertical ones, are automatically compensated without you noticing.

If the background is reality though, it's way different. The eyes calibrate to the background. And then if you render misaligned images, the two rendered images will not combine into one in the brain. Or in case of very small errors, it will, but it will look blurry, almost as if the lens are wrong, or dirty. It looks very similar to how astigmatism looks like without glasses.

Here's how it should look (small cross rendered with a big building in the background):

And here is how it looks if the lens are a tiny bit misaligned:

Doing the calibration was not easy; determining if a picture is blurry or not is not very precise, especially since I think my glasses are not strong enough for my right eye.

Instead, I had to render the small cross at infinite distance, but only to one eye at a time, and switched the eye twice a second. Then looked at a very distant building, and saw if the cross was moving or not. Once calibrated, it does not move.

Side note: Astigmatism

By the way, get yourself checked for astigmatism. It's something that's compensated very well by the brain, so you don't even notice, but reading or looking at screens gets more and more tiring.

The other interesting effect is that the image is clear if you're looking at it with both eyes, but it's blurry when looking with one eye closed.

Also, astigmatism doesn't look like this:

This is just a dirty windshield. A fake and misleading image.

It looks much more like this, a completely linear (and not gaussian) blur:

Notice how the arrows seems a bit "doubled", a typical characteristic of astigmatism.

It took way too long for me to figure out I have it (even though both my parents have corrective lenses for it). Seeing is so much easier since I got glasses.

And I look cooler too.

If you need Augmented Reality problem solving, or want help implementing an AR or VR idea, drop us a mail at info@voidcomputing.hu